|
为什么无论多高的雨滴落下来都有一个不大的末速度?普通物理课会告诉学生,因为雨滴在下落时会受到与速度正相关的空气阻力,导致雨滴的下落末速度趋于某个定值。但这个阻力与速度的关系是怎样的呢?一百七十年前,爱尔兰物理学家斯托克斯对类似的问题产生了兴趣,并提出了在小雷诺数条件下流体阻力与速度成正比的斯托克斯定律。斯托克斯当时又是如何推导的呢?
10月6日14时,《张朝阳的物理课》第二百二十五期开播,搜狐创始人、董事局主席兼首席执行官、物理学博士张朝阳坐镇搜狐视频直播间,从流体力学最基本的纳维尔-斯托克斯方程(Navier-Stokes equations,下文简称NS方程)出发,“马拉松”式地一步步推导出斯托克斯定律,课堂全程持续近5个小时。

回顾雨滴下落速度的求解
假设有一个密度为ρ_d的球形雨滴,它在密度为ρ_a的空气中从静止开始下落,这个过程中雨滴会受到三个力:向下的重力G、向上的空气浮力F_{浮}和向上的空气阻力Fₛ,其中空气阻力满足斯托克斯定律,将它们依次写出来是
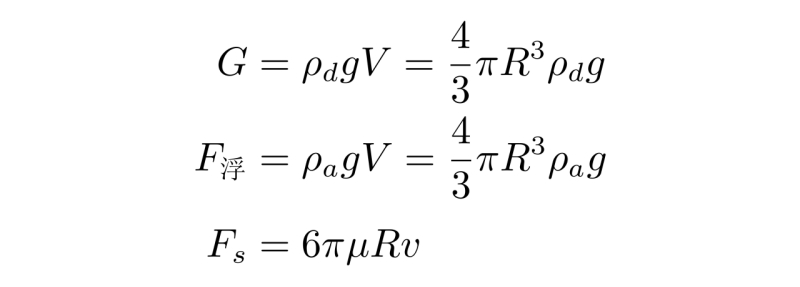
注意看最后一个式子所描述的空气阻力,它正是斯托克斯定律所给出的表达式,其中μ是空气的粘滞系数,R是雨滴半径,v是雨滴相对空气的速度,这三个量的一次方相乘再乘以6π就得到了球形物体在不可压缩定常流体中所受到的阻力。本节课的任务,正是从基本的流体力学最基本的NS方程出发,推导出斯托克斯定律。不过在进入正题前,先看看斯托克斯定律在雨滴下落情景中发挥的作用。
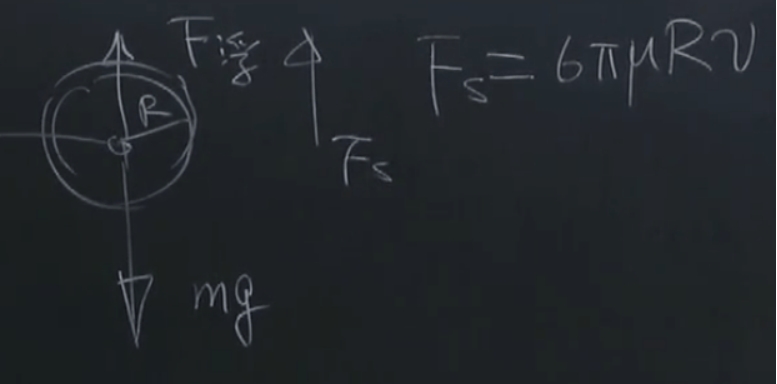
(对雨滴的受力分析)
由刚刚分析出的三个力可以写下雨滴的运动方程
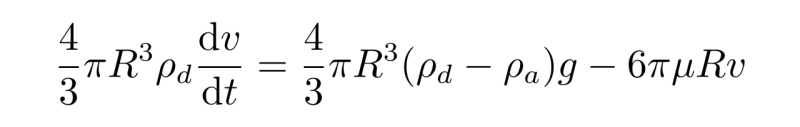
为了化简方程,可以将系数用两个字母代替
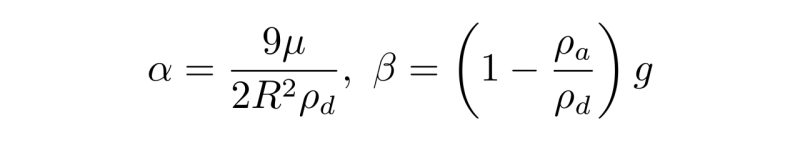
这样就能把雨滴运动方程化简为
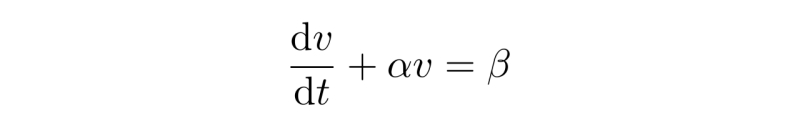
可以猜测这个微分方程的解具有如下形式
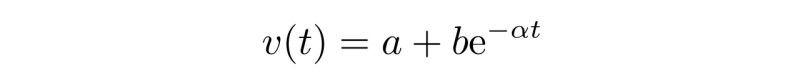
代回原方程,得到
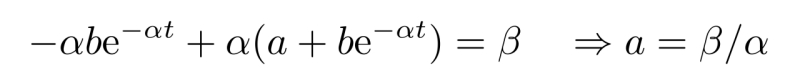
再考虑到初始条件,即雨滴在零时刻静止,可以得到
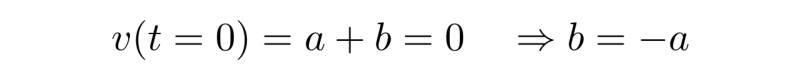
所以
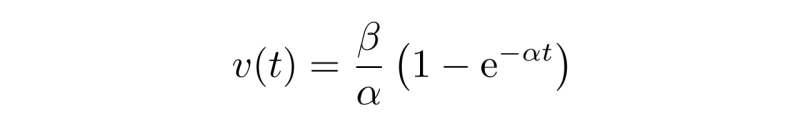
和自由落体的速度线性增长不同的是,在考虑空气阻力的情况下,雨滴的下落速度在t→∞时无限逼近一个有限值,它就是雨滴下落的最终速度
|
 茂栋在线
茂栋在线 茂栋在线
茂栋在线


